一致性协议：Bully

Bully 是最常用的一种领导选举算法，它使用节点 ID 的大小来选举新领导者。在所有活跃的节点中，选取节点 ID 最大或者最小的节点为主节点。

核心算法

每个节点都会获得分配给它的唯一 ID。在选举期间，ID 最大的节点成为领导者。因为 ID 最大的节点“逼迫”其他节点接受它成为领导者，它也被称为君主制领导人选举：类似于各国王室中的领导人继承顺位，由顺位最高的皇室成员来继承皇位。如果某个节点意识到系统中没有领导者，则开始选举，或者先前的领导者已经停止响应请求。

算法核心如下：

集群中每个活着的节点查找比自己 ID 大的节点，如果不存在则向其他节点发送 Victory 消息，表明自己为领导节点。
如果存在比自己 ID 大的节点，则向这些节点发送 Election 消息，并等待响应。
如果在给定的时间内，没有收到这些节点回复的消息，则自己成为领导节点，并向比自己 ID 小的节点发送 Victory 消息。
节点收到比自己 ID 小的节点发送的 Election 消息，则回复 Alive 消息。

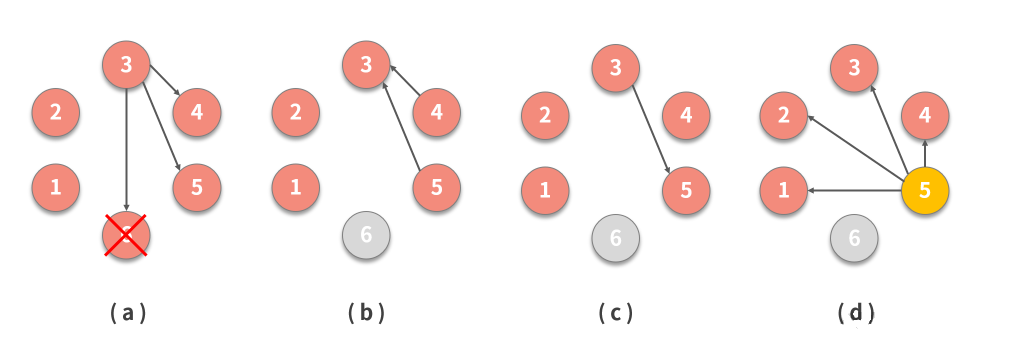
上图举例说明了 Bully 领导者选举算法，其中：

节点3 注意到先前的领导者 6 已经崩溃，并且通过向比自己 ID 更大的节点发送选举消息来开始新的选举。
4 和 5 以 Alive 响应，因为它们的 ID 比 3 更大。
3 通知在这一轮中作出响应的最大 ID 节点是5。
5 被选为新领导人，它广播选举信息，通知排名较低的节点选举结果。

这种算法的一个明显问题是：它违反了“安全性”原则（即一次最多只能选出一位领导人）。在存在网络分区的情况下，在节点被分成两个或多个独立工作的子集的情况下，每个子集都会选举其领导者。（脑裂）

该算法的另一个问题是：**它对 ID较大的节点有强烈的偏好，但是如果它们不稳定，会严重威胁选举的稳定性，并可能导致不稳定节点永久性地连任。**即不稳定的高排名节点提出自己作为领导者，不久之后失败，但是在新一轮选举中又赢得选举，然后再次失败，选举过程就会如此重复而不能结束。这种情况，可以通过监控节点的存活性指标，并在选举期间根据这些指标来评价节点的活性，从而解决该问题。

算法改进

Bully 算法虽然经典，但由于其相对简单，在实际应用中往往不能得到良好的效果。因此在分布式数据库中，我们会看到如下所述的多种演进版本来解决真实环境中的一些问题，但需要注意的是，其核心依然是经典的 Bully 算法。

故障转移节点列表

**我们可以使用多个备选节点作为在发生领导节点崩溃后的故障转移目标，从而缩短重选时间。**每个当选的领导者都提供一个故障转移节点列表。当集群中的节点检测到领导者异常时，它通过向该领导节点提供的候选列表中排名最高的候选人发送信息，开始新一轮选举。如果其中一位候选人当选，它就会成为新的领导人，而无须经历完整的选举。

如果已经检测到领导者故障的进程本身是列表中排名最高的进程，它可以立即通知其他节点自己就是新的领导者。

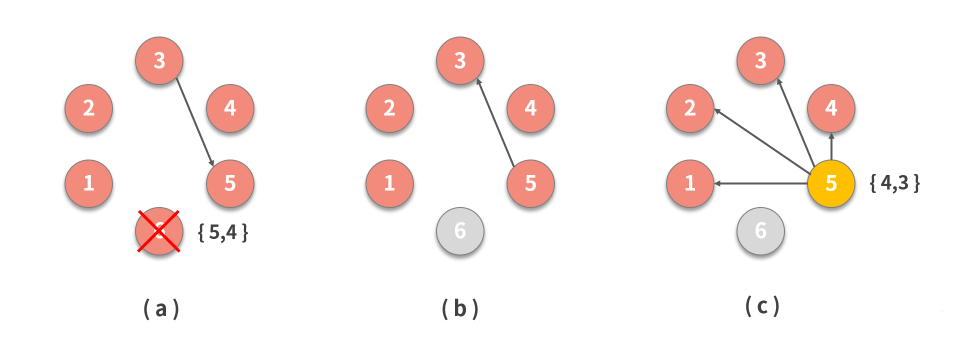
上图显示了采用这种优化方式的过程，其中：

6 是具有指定候选列表 {5，4} 的领导者，它崩溃退出，3 注意到该故障，并与列表中具有最高等级的备选节点5 联系；
5 响应 3，表示它是 Alive 的，从而防止 3 与备选列表中的其他节点联系；
5 通知其他节点它是新的领导者。

如果备选列表中，第一个节点是活跃的，我们在选举期间需要的步骤就会更少。

节点分角色

另一种算法试图通过将节点分成候选和普通两个子集来降低消息数量，其中只有一个候选节点可以最终成为领导者。普通节点联系候选节点、从它们之中选择优先级最高的节点作为领导者，然后将选举结果通知其余节点。

为了解决并发选举的问题，该算法引入了一个随机的启动延迟，从而使不同节点产生了不同的启动时间，最终导致其中一个节点在其他节点之前发起了选举。该延迟时间通常大于消息在节点间往返时间。具有较高优先级的节点具有较低的延迟，较低优先级节点延迟往往很大。

上图显示了选举过程的步骤，其中：

节点 4 来自普通的集合，它发现了崩溃的领导者 6，于是通过联系候选集合中的所有剩余节点来开始新一轮选举；
候选节点响应并告知 4 它们仍然活着；
4 通知所有节点新的领导者是 2。

该算法减小了领导选举中参与节点的数量，从而加快了在大型集群中该算法收敛的速度。

邀请算法

**邀请算法允许节点“邀请”其他进程加入它们的组，而不是进行组间优先级排序。**该算法允许定义多个领导者，从而形成每个组都有其自己的领导者的局面。每个节点开始时都是一个新组的领导者，其中唯一的成员就是该节点本身。

组领导者联系不属于它们组内的其他节点，并邀请它们加入该组。如果受邀节点本身是领导者，则合并两个组；否则，受邀节点回复它所在组的组长 ID，允许两个组长直接取得联系并合并组，这样大大减少了合并的操作步骤。

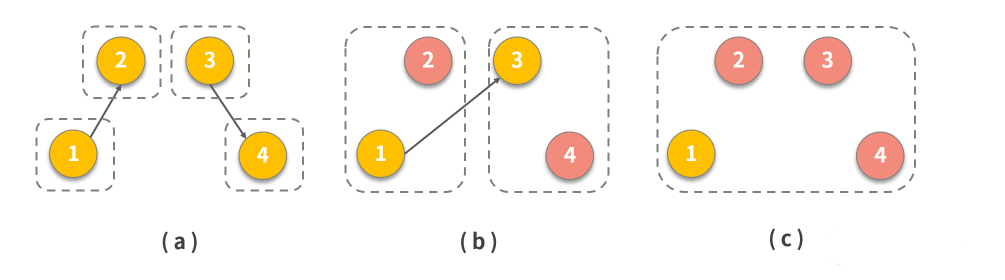
上图显示了邀请算法的执行步骤，其中：

四个节点形成四个独立组，每个节点都是所在组的领导，1 邀请 2 加入其组，3 邀请 4 加入其组；
2 加入节点 1的组，并且 4 加入节点3的组，1 为第一组组长，联系人另一组组长 3，剩余组成员（在本例中为 4个）获知了新的组长 1；
合并两个组，并且 1 成为扩展组的领导者。

由于组被合并，不管是发起合并的组长成为新的领导，还是另一个组长成为新的领导。为了将合并组所需的消息数量保持在最小，一般选择具有较大 ID 的组长的领导者成为新组的领导者，这样，只有来自较小 ID 组的节点需要更新领导者。

与所讨论的其他算法类似，该算法采用“分而治之”的方法来收敛领导选举。邀请算法允许创建节点组并合并它们，而不必从头开始触发新的选举，这样就减少了完成选举所需的消息数量。

环形算法

**在环形算法中，系统中的所有节点形成环，并且每个节点都知道该环形拓扑结构，了解其前后邻居。**当节点检测到领导者失败时，它开始新的选举，选举消息在整个环中转发，方式为：每个节点联系它的后继节点（环中离它最近的下一节点）。如果该节点不可用，则跳过该节点，并尝试联系环中其后的节点，直到最终它们中的一个有回应。

节点联系它们的兄弟节点，收集所有活跃的节点从而形成可用的节点集。在将该节点集传递到下一个节点之前，该节点将自己添加到集合中。

该算法通过完全遍历该环来进行。当消息返回到开始选举的节点时，从活跃集合中选择排名最高的节点作为领导者。

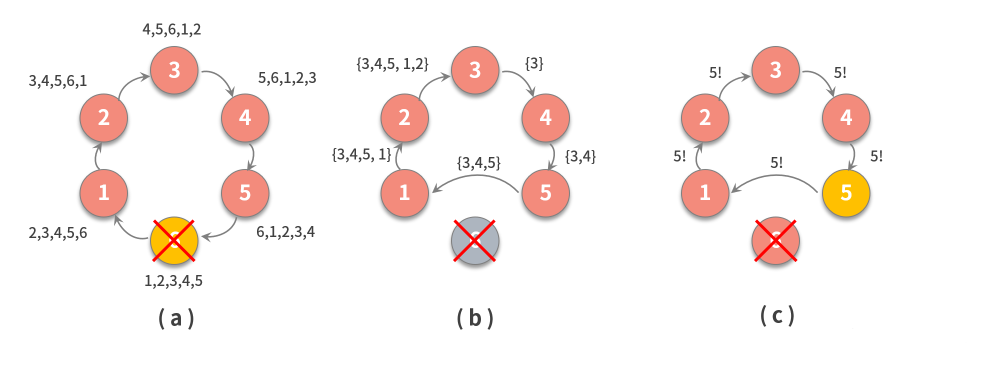
如上图所示，你可以看到这样一个遍历的例子：

先前的领导 6 失败了，环中每个节点都从自己的角度保存了一份当前环的拓扑结构；
以 3 为例，说明查找新领导的流程，3 通过开始遍历来发起选举轮次，在每一步中，节点都按照既定路线进行遍历操作，5 不能到 6，所以跳过，直接到 1；
由于 5 是具有最高等级的节点，3 发起另一轮消息，分发关于新领导者的信息。

该算法的一个优化方法是每个节点只发布它认为排名最高的节点，而不是一组活跃的节点，以节省空间：因为 Max 最大值函数是遵循交换率的，也就是知道一个最大值就足够了。当算法返回到已经开始选举的节点时，最后就得到了 ID 最大的节点。

另外由于环可以被拆分为两个或更多个部分，每个部分就会选举自己的领导者，这种算法也不具备“安全性”。 如前所述，要使具有领导的系统正常运行，我们需要知道当前领导的状态。因此，为了系统整体的稳定性，领导者必须保证是一直活跃的，并且能够履行其职责。

脑裂的解决方案

在上文讨论的所有算法都容易出现脑裂的问题，即最终可能会在独立的两个子网中出现两个领导者，而这两个领导并不知道对方的存在。

为了避免脑裂问题，我们一般需要引入法定人数来选举领导。比如 Elasticsearch 选举集群领导，就使用 Bully 算法结合最小法定人数来解决脑裂问题。

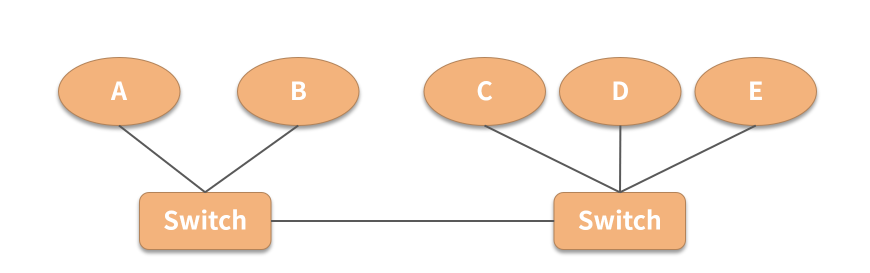
如上图所示，目前有 2 个网络、5 个节点，假定最小法定人数是3。A 目前作为集群的领导，A、B 在一个网络，C、D 和 E 在另外一个网络，两个网络被连接在一起。

当这个连接失败后，A、B 还能连接彼此，但与 C、D 和 E 失去了联系。同样， C、D 和 E 也能知道彼此，但无法连接到 A 和B。

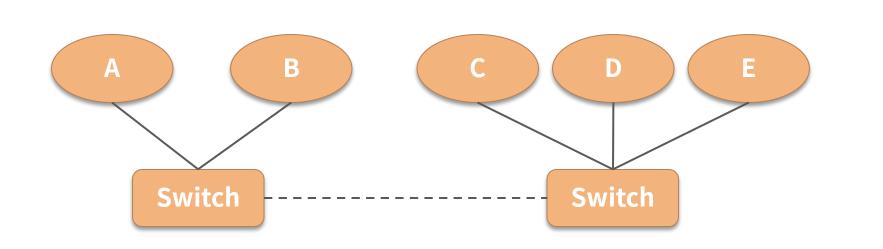
此时，C、D 和 E 无法连接原有的领导 A。同时它们三个满足最小法定人数3，故开始进行新一轮的选举。假设 C 被选举为新的领导，这三个节点就可以正常进行工作了。

而在另外一个网络中，虽然 A 是曾经的领导，但是这个网络内节点数量是 2，小于最小法定人数。故 A 会主动放弃其领导角色，从而导致该网络中的节点被标记为不可用，从而拒绝提供服务。这样就有效地避免了脑裂带来的问题。