存储与检索
核心存储结构
哈希
K-V 存储与大多数编程语言所内置的字典结构非常相似,通常采用哈希表(hash table) 来实现。那如果我们想将其拓展到磁盘存储索引,该如何去做呢?
保存内存中的哈希表,把每个键一一映射到数据文件中特定的字节偏移,这样就可以找到每个值的位置。 每当在文件中追加新的数据,还要更新哈希表来反映刚刚写入数据的偏移量 (包括插入新的键和更新已有的键)。 查找某个值时,使用哈希表来找到文件中的偏移量,即存储位置,然后读取其内容。
只要所有的 key 可以放入内存(因为哈希表需要保存在内存中),value 的数据量则可以超过内存大小,只需一次磁盘寻址,就可以将 value 从磁盘加载到内存。 如果那部分数据文件已经在文件系统的缓存中,则读取根本不需要任何的磁盘 I/O。
如果只追加到一个文件,那么很有可能导致磁盘空间用尽。因此通常将日志分解成一定大小的段,当文件达到一定大小时就关闭它,井将后续写入到新的段文件中。
此外,由于压缩往往使得段更小(假设键在段内被覆盖多次),也可以在执行压缩的同时将多个段合并在一起。
每个段现在都有自己的内存哈希表,将键映射到文件的偏移量。为了找到键的值,首先检查最新的段的哈希表;如果键不存在,检查第二最新的段,以此类推。由于合并过程可以维持较少的段数,因此查找通常不需要检查很多哈希表。
优点:
- 追加和分段合并主要是顺序写,它通常比随机写入快得多,特别是在 HDD 上。
- 如果段文件是追加的或不可变的,则并发和崩溃恢复要简单得多。
- 合并旧段可以避免随着时间的推移数据文件出现碎片化的问题
缺点:
- 哈希表必须全部放入内存,随着数据越来越多,哈希冲突解决的成本会越来越高。
- 区间查询效率不高。
SSTable与LSM-Tree
将日志结构的存储段中的 key-value 顺序按键排序。这种结构称为排序字符串表(SSTable)。它要求每个键在每个合并的段文件中只能出现一次。
SSTable 相比哈希索引的日志段,具有以下优点:
- 合并段更加简单高效,即使文件大于可用内存。
- 在文件中查找特定的键时,不再需要在内存中保存所有键的索引。
- 由于读请求往往需要扫描请求范围内的多个 key-value 对,可以考虑将这些记录保存到一个块中并在写磁盘之前将其压缩。
SSTable的构建与维护
基本工作流程如下:
-
当写入时,将其添加到内存中的平衡树数据结构中(例如红黑树)。这个内存中的树有时被称为内存表。
-
当内存表大于某个阈值(通常为几兆字节)时,将其作为 SSTable 文件写入磁盘。由于树已经维护了按键排序的 key-value 对, 磁盘可以比较高效。新的 SSTable 文件成为数据库的最新部分。当 SSTable 写磁盘的同时,写入可以继续添加到一个新的内存表实例。
-
为了处理读请求,首先尝试在内存表中查找键,然后是最新的磁盘段文件,接下来是次新的磁盘段文件,以此类推,直到找到目标(或为空)。
-
后台进程周期性地执行段合并与压缩过程,以合并多个段文件,并丢弃那些已被覆盖或删除的值。
如果数据库崩溃,最近的写入(在内存表中但尚未写入磁盘)将会丢失。为了避免该问题,可以在磁盘上保留单独的日志(WAL 日志),每个写入都会立即追加到该日志。每当将内存表写入 SSTable 时,则相应的日志可以被丢弃。
优化
LSM-Tree 的一些优化措施如下:
- 布隆过滤器:在确定键不存在之前,必须先检查内存表,然后将段一直回溯访问到最旧的段文件(可能必须从磁盘多次读取)。为了优化这种访问,存储引擎通常使用额外的布隆过滤器,其用于近似计算集合的内容。如果数据库中不存在某个键,它能够很快告诉你结果,从而节省了很多对于不存在的键的不必要的磁盘读取。
- 分层压缩与大小分级:在大小分级的压缩中,较新的和较小的 SSTable 被连续合并到较旧和较大的 SSTable 。在分层压缩中,键的范围分裂成多个更小的 SSTable,旧数据被移动到单独的层级,这样压缩可以逐步进行并节省磁盘空间。
B-Tree
B-Tree 将数据库分解成固定大小的块或页(页是内部读/写的最小单元),传统页的大小为 4 KB。这种设计更接近底层硬件,因为磁盘也是以固定大小的块排列。
每个页面都可以使用地址或位置进行标识,这样可以让一个页面引用另一个页面,类似指针,不过是指向磁盘地址,而不是内存。

某一个页被指定为 B-Tree 的根,每当查找索引中的一个键时,总是从这里开始。该页面包含若干个键和对子页的引用。每个孩子都负责一个连续范围内的键,相邻引用之间的键可以指示这些范围之间的边界。
例如上图即是一个查询,假定正在查找键 251,因此需要沿着 200~300 间的页引用,到达类似的页,它进一步将 200~300 范围分解成子范围。最终,我们到达一个包含单个键的页(叶子页),该页包含每个内联键的值或包含可以找到值的页的引用。

如上图。如果要更新 B-Tree 中现有键的值,首先搜索包含该键的叶子页,更改该页的值,并将页写回到磁盘(对该页的任何引用仍然有效)。如果要添加新键,则需要找到其范围包含新键的页,并将其添加到该页。如果页中没有足够的可用空间来容纳新键,则将其分裂为两个半满的页,并且父页也需要更新以包含分裂之后的新的键范围。
预写日志
为了使数据库能从崩溃中恢复,常见 B-Tree 实现需要支持磁盘上的额外的数据结构:预写日志(write-ahead log, WAL )也称重做日志(Redo-log)。这是一个仅支持追加修改的文件,每个 B-tree 的修改必须先更新 WAL 然后再修改树本身的页。当数据库在崩溃后需要恢复 ,该日志用于将B-tree 恢复到最近一直的状态。
优化
B-Tree 常见的一些优化措施如下:
- 一些数据库(如 LMDB)不使用覆盖页和维护 WAL 来进行崩溃恢复,而是使用写时拷贝方案 。 修改的页被写入不同的位置,树中父页的新版本被创建,并指向新的位置。
- 保存键的缩略信息,而不是完整的键,这样可以节省页空间。 特别是在树中间的页中,只需要提供足够的信息来描述键的起止范围。这样可以将更多的键压入到页中,让树具有更高的分支因子,从而减少层数。
- 许多 B-Tree 的实现尝试对树进行布局,以便相邻叶子页可以按顺序保存在磁盘上。 这主要由于页可以放在磁盘上的任何位置;没有要求相邻的页需要放在磁盘的相邻位置。如果查询需要按照顺序扫描大段的键范围,考虑到每个读取的页都可能需要磁盘 I/O,所以逐页的布局可能是低效的。
- 添加额外的指针到树中。 例如,每个叶子页面可能会向左和向右引用其同级的兄弟页,这样可以顺序扫描键,而不需要跳回到父页。
- B-Tree 的变体如分形树借鉴了一些日志结构的想法也来减少磁盘寻道。
事务处理与分析处理
即使数据库开始被用于许多不同类型的数据,比如博客文章的评论,游戏中的动作,地址簿中的联系人等等,基本的访问模式仍然类似于处理商业交易。应用程序通常使用索引通过某个键查找少量记录。根据用户的输入插入或更新记录。由于这些应用程序是交互式的,这种访问模式被称为在线事务处理(OLTP, OnLine Transaction Processing)。
数据库也开始越来越多地用于数据分析,这些数据分析具有非常不同的访问模式。通常,分析查询需要扫描大量记录,每个记录只读取几列,并计算汇总统计信息(如计数、总和或平均值),形成报告以帮助公司管理层做出更好的决策(商业智能)。这种访问模式被称为在线分析处理(OLAP, OnLine Analytice Processing)。
OLTP 和 OLAP 之间的区别如下:
| 属性 | 事务处理 OLTP | 分析处理 OLAP |
|---|---|---|
| 主要读取模式 | 查询少量记录,按键读取 | 在大批量记录上聚合 |
| 主要写入模式 | 随机访问,写入要求低延时 | 批量导入(ETL)或者事件流 |
| 主要用户 | 终端用户,通过Web应用 | 内部数据分析师,用于决策支持 |
| 处理的数据 | 数据的最新状态(当前时间点) | 随时间推移的历史事件 |
| 数据集尺寸 | GB ~ TB | TB ~ PB |
数据仓库
起初,事务处理和分析查询使用了相同的数据库。 SQL 被证明是非常灵活的,可以同时胜任 OLTP 类型和OLAP 类型查询 。尽管如此,在二十世纪八十年代末和九十年代初期,企业有停止使用 OLTP 系统进行分析的趋势,转而在单独的数据库上运行分析。这个单独的数据库被称为数据仓库(data warehouse)。
考虑到直接在 OLTP 数据库上运行临时的分析查询的开销特别大(会扫描大部分数据集),这可能会损害并发执行事务的性能。因此,数据仓库是一个独立的数据库,分析人员可以查询他们想要的内容而不影响 OLTP 操作。
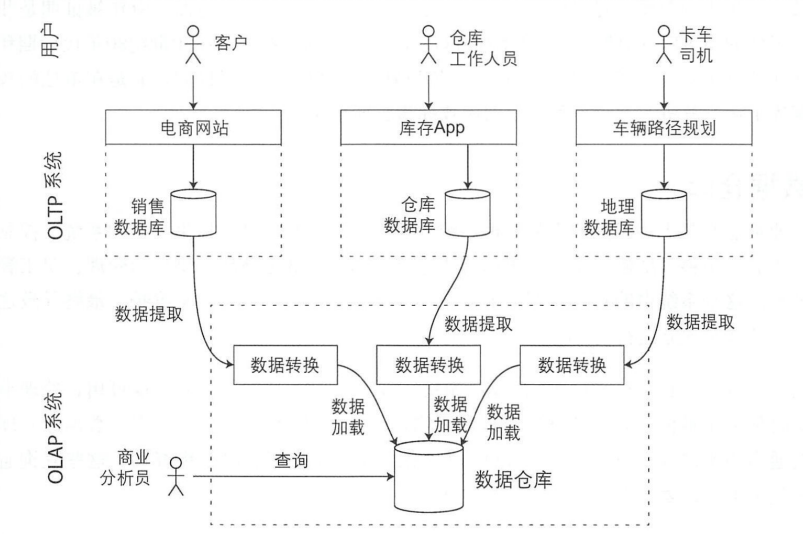
数据仓库包含公司各种 OLTP 系统中所有的只读数据副本。从 OLTP 数据库中提取数据(使用定期的数据转储或连续的更新流),转换成适合分析的模式,清理并加载到数据仓库中。将数据存入仓库的过程称为抽取-转换-加载(ETL)。具体流程如下图所示:
雪花模型与星型模型
事实表的每一行代表在特定时间发生的事件。而它的一些列是属性,例如产品销售的价格和从供应商那里购买的成本(可以用来计算利润余额)。其他列可能会引用其他表的外键,称为维度表。由于事实表中的每一行都代表一个事件,维度通常代表事件的对象(who)、什么(what)、地点(where)、时间(when)、方法(how)以及原因(why)。
星型模式这个名字的来源是当我们对表之间的关系进行可视化时,事实表在中间,被维度表包围;与这些表的连接就像星星的光芒。例如下图:
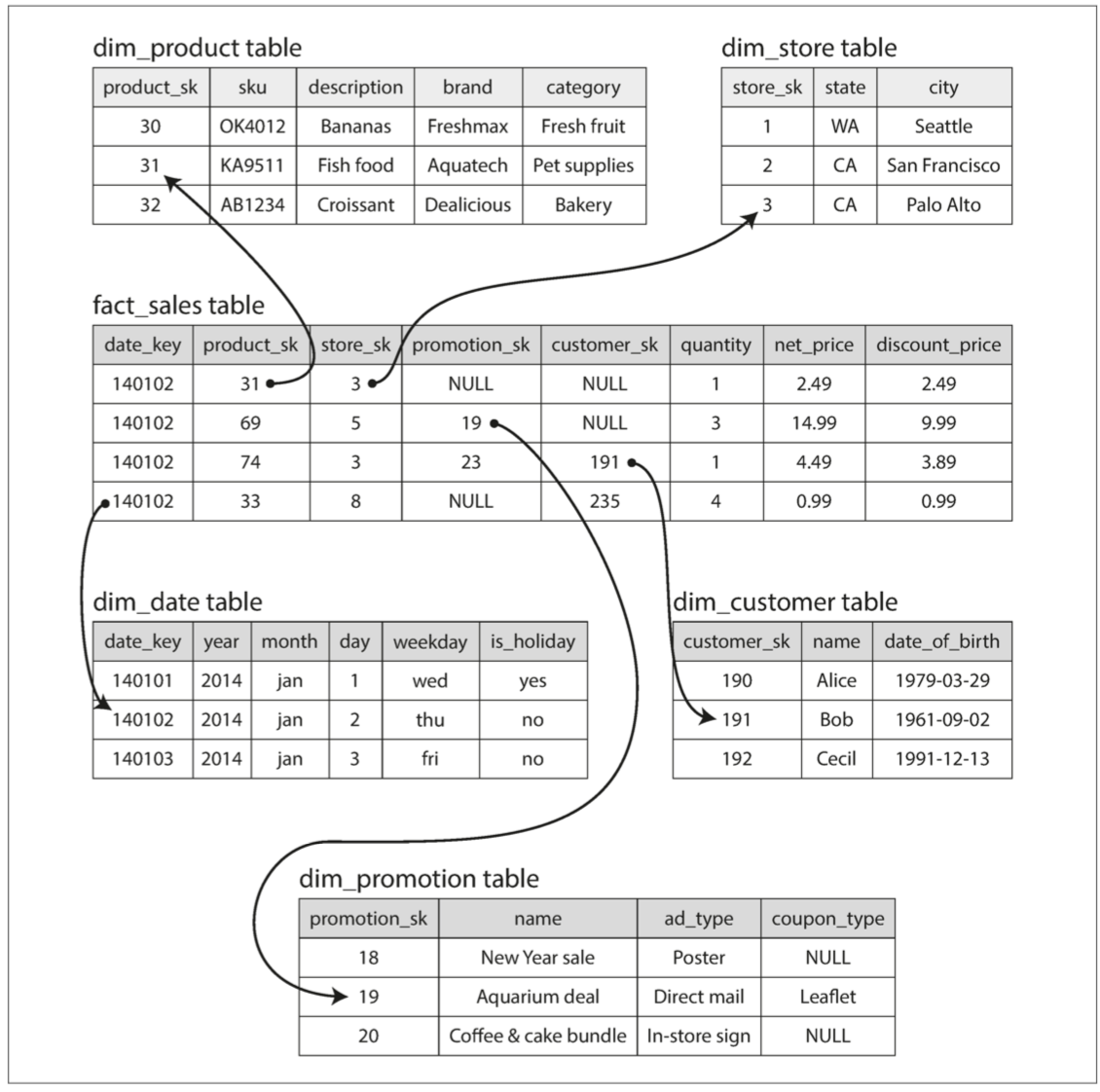
这个模板的变体被称为雪花模式,维度被进一步分解为子维度。例如,品牌和产品类别可能有单独的表格,并且 dim_product 表格中的每一行都可以将品牌和类别作为外键引用,而不是将它们作为字符串存储在 dim_product 表格中。雪花模式比星形模式更规范化,但是星形模式通常是首选,因为它使用起来更简单。
列式存储
在传统的按行存储的数据库中,当用户需要查询某个特定列的时候,即使我们已经建立了索引,但是存储引擎仍然会将这些行数据(可能有上百个字段)完整的从硬盘加载到内存中,并对它们进行解析、条件过滤,这需要花费大量的时间。在一些大数据的场景下,事实表中可能会有万亿行和数 PB 的数据,此时按行存储很明显是不可用的。
列式存储背后的想法很简单:不要将所有来自一行的值存储在一起,而是将来自每一列的所有值存储在一起。如果每个列存储在一个单独的文件中,查询只需要读取和解析查询中使用的那些列,这可以节省大量的工作,如下图所示:

列式存储布局依赖于一组列文件,每个列文件以相同顺序的顺序存储行数据。 因此,如果需要重新组装完整的行,可以从每个单独的列文件中获取对应的那一行,并将它们放在一起形成完整的行。
压缩
由于同一列中的数据类型相同,因此我们可以通过压缩数据来进一步降低对硬盘吞吐量的要求。在数据仓库中,通常使用位图编码来压缩数据:

通常情况下,一列中不同值的数量要远远小于它的行数。我们假设某一列中有 n 种不同的值,此时我们就可以将其转换为 n 个位图,位图中对应位置用 0 和 1 标识该行是否存在这个值(即列中每个值对应一个位图,每行对应一个比特位)。
考虑到 n 可能会很大,此时位图中存储的 1 可能会较为稀疏(浪费空间),这时就可以另外对位图进行游程编码,如图的下半部分所示。
内存带宽:对于需要扫描数百万行的数据仓库查询来说,一个巨大的瓶颈是从硬盘获取数据到内存的带宽。但是,这不是唯一的瓶颈。分析型数据库的开发人员还需要有效地利用主存储器到 CPU 缓存的带宽,避免 CPU 指令处理流水线中的分支预测错误和气泡,以及在现代 CPU 上使用单指令多数据(SIMD)指令。
矢量化处理:列式存储布局可以更有效的利用 CPU 周期。查询引擎可以将大量压缩的列数据放在 CPU 的 L1 缓存中,然后在紧密的循环(即没有函数调用)中遍历。相比较于每个记录的处理都需要大量函数调用和条件判断的代码,CPU 执行这样一个循环要快得多。列压缩允许列中的更多行被放进相同数量的 L1 缓存。前面描述的按位 “与” 和 “或” 运算符可以被设计为直接在这样的压缩列数据块上操作。
排序
对于列式存储来说,按照插入顺序来存储数据是最简单的,因为我们只需要将插入行的数据追加到各个列文件中即可。但是考虑到查询、压缩的效率,通常我们会选择几个列作为排序列,所有列文件以该列为标准来排序数据。
最常见的做法是依据我们的查询条件来指定,例如在经常以时间来筛选的场景,就可以将时间设定为第一个排序 key,这样在查询的时候,我们就能够缩小扫描的范围,只锁定对应时间周期的数据。接着,我们可以将数据的特征等信息作为第二、三个排序 key,这样就能够帮助我们更加精准的进行查询、分组、聚合。
排序还有另一个好处,就是在排序完成后,相同的数据会连续存储。这时再采用一些压缩算法(例如前面提到的游程编码),就可以极大的节省空间。
写入
对于列式存储来说,使用类似于 B+ 树那样原地更新的方法是不可行的,这不仅意味着我们需要先对数据进行解码,如果数据插入在中间位置,还需要在全部列文件中向后偏移该行以后的所有数据,效率十分低下。
基于以上原因,列式存储通常采用类似 LSM 树那样的存储结构。即所有的写入首先会存储到内存中的 MemTable 中(红黑树、跳表、AVL 树等结构),当 MemTable 达到一定的大小后,此时就会将数据写入到磁盘中,与原有的列数据进行合并(保留最新的),并批量写入到新文件中。
在查询的时候其实也是分别查询磁盘结构和内存结构后合并查询结果,但是查询优化器向用户隐藏了这个细节。
聚合:物化视图与数据立方体
数据仓库的查询通常会涉及聚合函数,如 SQL 中的 COUNT、SUM、AVG、MIN 或 MAX。为了避免每次查询时都对原始数据进行一次聚合计算,通常会将一些频繁使用的聚合结果给缓存下来。
创建这种缓存的一种方式是物化视图(Materialized View)。在关系数据模型中,它通常被定义为一个标准(虚拟)视图:**一个类似于表的对象,其内容是一些查询的结果。**不同的是,物化视图是查询结果的实际副本,会被写入硬盘,而虚拟视图只是编写查询的一个捷径。从虚拟视图读取时,SQL 引擎会将其展开到视图的底层查询中,然后再处理展开的查询。
当底层数据发生变化时,物化视图就需要更新,因为它是数据的非规范化副本。虽然数据库可以自动完成该操作,但是这样的更新使得写入的成本更高,这就是在 OLTP 数据库中不经常使用物化视图的原因,而在读取频繁的 OLAP 数据仓库中,它们的作用就体现了出来。
物化视图常见的一种特殊实现被称为数据立方体或 OLAP 立方体,它是按不同维度分组的聚合网格,如下图所示:

数据立方体的优点是其提前计算好了一些聚合的结果,可以让一些查询变得非常快,但同时也因为它没有保留原始数据,不具有查询原始数据的灵活性,所以它通常作为提升查询性能的优化手段。