权重计算原理

在Elasticsearch中，每个文档都有相关性评分，用一个正浮点数字段 _score 来表示 。 _score 的评分越高，相关性越高。为了保证搜索到的结果相关度更高，在默认情况下返回结果会按照相关度降序排序。

Elasticsearch使用布尔模型查找匹配文档，并用一个名为实用评分函数的公式来计算相关度。这个公式借鉴了词频/逆向文档频率和向量空间模型，同时也加入了一些现代的新特性，如协调因子，字段长度归一化，以及词或查询语句权重提升。

布尔模型

布尔模型（Boolean Model） 适用于在查询中使用 AND 、 OR 和 NOT （与、或、非）这样的条件来查找匹配的文档，如以下查询：

1

full AND text AND search AND (elasticsearch OR lucene)

会将所有包括词 full 、 text 和 search ，以及 elasticsearch 或 lucene 的文档作为结果集。

这个过程简单且快速，它将所有可能不匹配的文档排除在外。

词频/逆向文档频率（TF/IDF）

Elasticsearch的相似度算法被定义为检索词频率/反向文档频率（TF/IDF），主要依赖以下内容

• 检索词频率

  • 检索词在该字段出现的频率。出现频率越高，相关性也越高。5次提到同一词的字段比只提到1次的更相关。

  • 词频的计算方式如下：

    1	tf(t in d) = √frequency

    词 t 在文档 d 的词频（ tf ）是该词在文档中出现次数的平方根。

• 逆向文档频率

  • 每个检索词在索引中出现的频率。频率越高，相关性越低。检索词出现在多数文档中会比出现在少数文档中的权重更低。

  • 逆向文档频率的计算公式如下：

    1	idf(t) = 1 + log ( numDocs / (docFreq + 1))

    词 t 的逆向文档频率（ idf ）是：索引中文档数量除以所有包含该词的文档数，然后求其对数。

• 字段长度归一值

  • 字段的长度。长度越长，相关性越低。 检索词出现在一个短的 title 要比同样的词出现在一个长的 content 字段权重更大。

  • 字段长度的归一值公式如下：

    1	norm(d) = 1 / √numTerms

    字段长度归一值（ norm ）是字段中词数平方根的倒数。

以上三个因素是在索引时计算并存储的。最后将它们结合在一起计算单个词在特定文档中的权重 。

向量空间模型

当然，查询通常不止一个词，所以需要一种合并多词权重的方式——向量空间模型（vector space model）。

向量空间模型（vector space model）提供一种比较多词查询的方式，单个评分代表文档与查询的匹配程度，为了做到这点，这个模型将文档和查询都以 向量（vectors） 的形式表示，而向量实际上就是包含多个数的一维数组，例如：

1

[1,2,5,22,3,8]

在向量空间模型里，向量空间模型里的每个数字都代表一个词的权重 ，与词频/逆向文档频率计算方式类似，下面举一个例子。

设想如果查询 “happy hippopotamus” ，常见词 happy 的权重较低，不常见词 hippopotamus 权重较高，假设 happy 的权重是 2 ， hippopotamus 的权重是 5 ，可以将这个二维向量—— [2,5] ——在坐标系下作条直线，线的起点是 (0,0) 终点是 (2,5) ，如下图

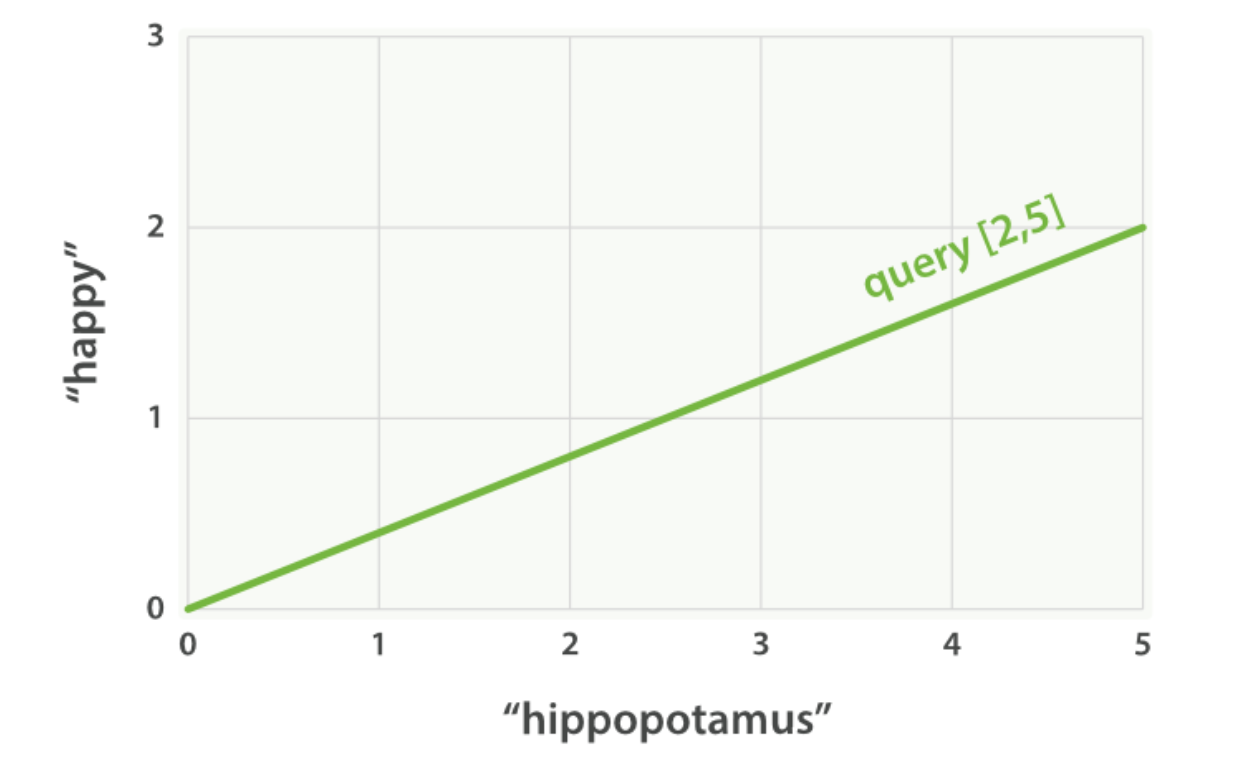
现在，设想我们有三个文档：

1. I am happy in summer 。
2. After Christmas I’m a hippopotamus 。
3. The happy hippopotamus helped Harry 。

三篇文档的命中词如下

• 文档 1： (happy,____________) —— [2,0]
• 文档 2： ( ___ ,hippopotamus) —— [0,5]
• 文档 3： (happy,hippopotamus) —— [2,5]

可以为每个文档都创建包括每个查询词—— happy 和 hippopotamus ——权重的向量，然后将这些向量置入同一个坐标系中，如下图

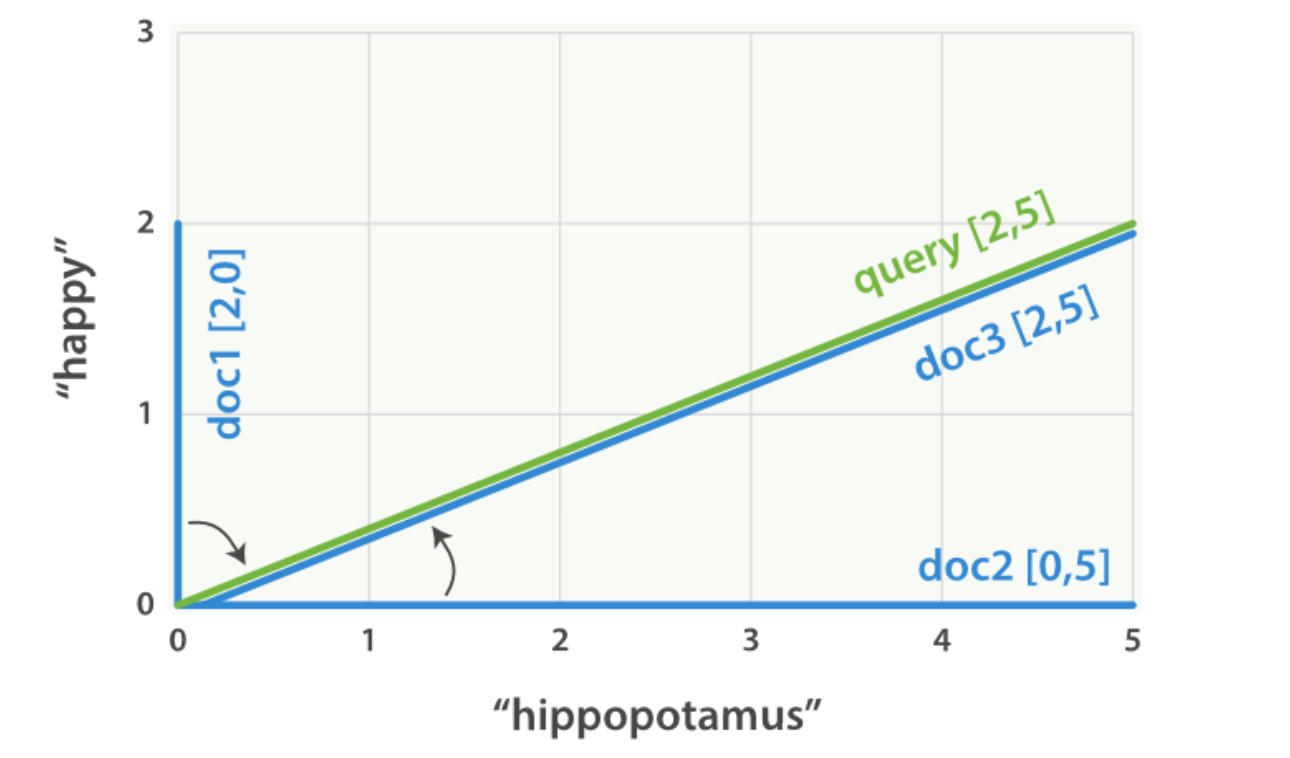
向量之间是可以比较的，只要测量查询向量和文档向量之间的角度就可以得到每个文档的相关度，文档 1 与查询之间的角度最大，所以相关度低；文档 2 与查询间的角度较小，所以更相关；文档 3 与查询的角度正好吻合，完全匹配。

在实际中，只有二维向量（两个词的查询）可以在平面上表示，幸运的是， 线性代数为我们提供了计算两个多维向量间角度工具，这意味着可以使用如上同样的方式来解释多个词的查询。